Temporal Score Rescaling for Temperature Sampling in Diffusion and Flow Models

Yanbo Xu*1, Yu Wu*1, Sungjae Park1, Zhizhou Zhou2, Shubham Tulsiani1
1Carnegie Mellon University, 2Stanford University
*Indicates Equal Contribution
Paper arXiv Code

Abstract

We present a mechanism to steer the sampling diversity of denoising diffusion and flow matching models, allowing users to sample from a sharper or broader distribution than the training distribution. We build on the observation that these models leverage (learned) score functions of noisy data distributions for sampling and show that rescaling these allows one to effectively control a 'local' sampling temperature. Notably, this approach does not require any finetuning or alterations to training strategy, and can be applied to any off-the-shelf model and is compatible with both, deterministic and stochastic samplers. We first validate our framework on toy 2D data, and then demonstrate its application for diffusion models trained across five disparate tasks -- image generation, pose estimation, depth prediction, robot manipulation, and protein design. We find that across these tasks, our approach allows sampling from sharper (or flatter) distributions, yielding performance gains e.g., depth prediction models benefit from sampling more likely depth estimates, whereas image generation models perform better when sampling a slightly flatter distribution.

Method

We propose Temporal Score Rescaling (TSR), a simple method that controls the likelihood-diversity trade-off for diffusion and flow models. TSR can be easily applied to any off-the-shelf diffusion or flow model, without any training or extra inference-time computation.

Given a pretrained diffusion model predicting noise $\epsilon_\theta(x,t)$ and parameter $k$ controlling the temperature, during the sampling process, TSR replaces $\epsilon_\theta(x,t)$ with a scaled prediction:

$$ \tilde{\epsilon}_\theta(x,t) = \frac{\alpha_t^2 \sigma^2 + \sigma_t^2}{\alpha_t \tfrac{\sigma^2}{k} + \sigma_t^2}~\epsilon_\theta(x,t) \equiv r_t(k, \sigma) \epsilon_\theta(x,t)$$

where $\alpha_t$, $\sigma_t$ are the diffusion noise schedule given by $x_t = \alpha_t x_0 + \sigma_t \epsilon$. $\sigma$ is a user-input parameter.

For a flow matching model predicting flow velocity $v_\theta(x,t)$, TSR replaces it with the following velocity:

$$ \tilde{v}_{\theta}(x,t) = \alpha_t^{-1}(r_t(k, \sigma)(\alpha_t v_\theta(x,t) - \dot{\alpha_t}x) + \dot{\alpha_t}x) $$

Steering Distribution with TSR

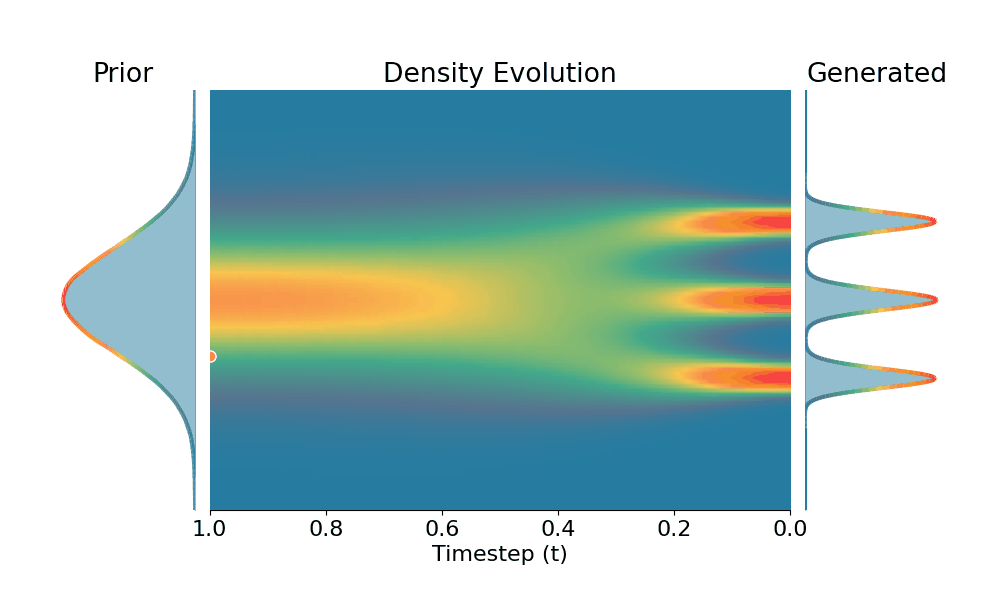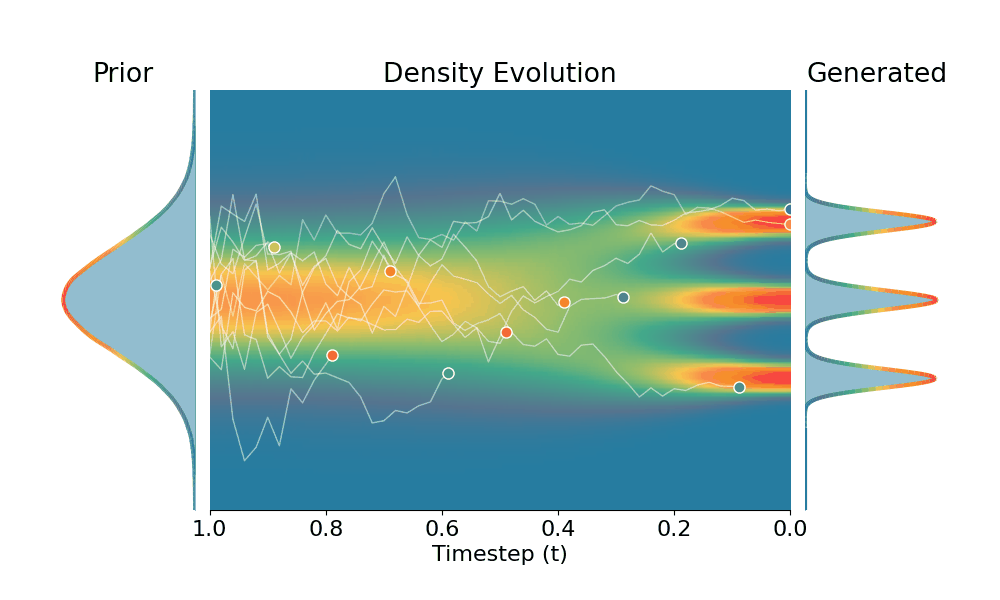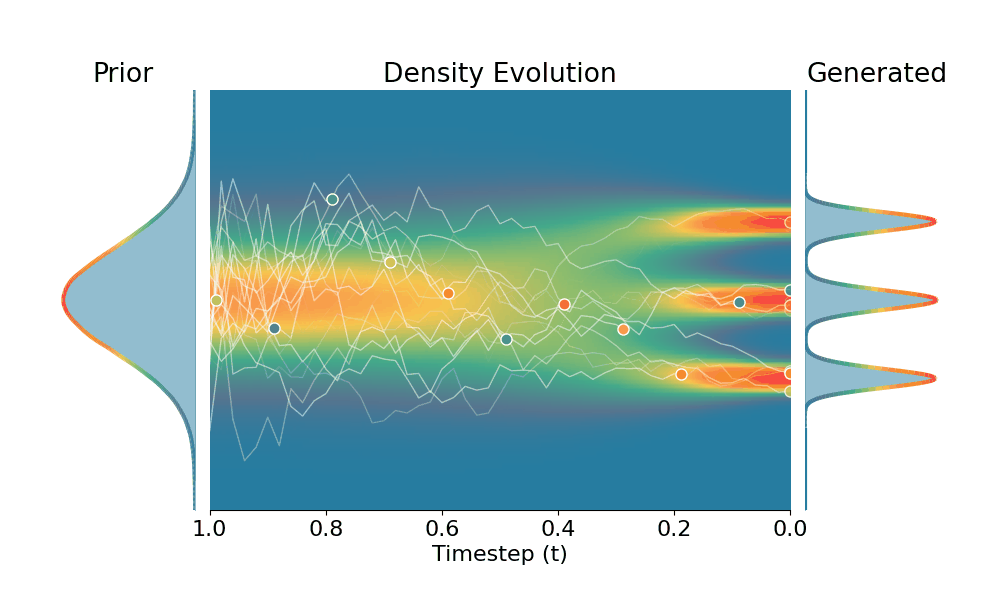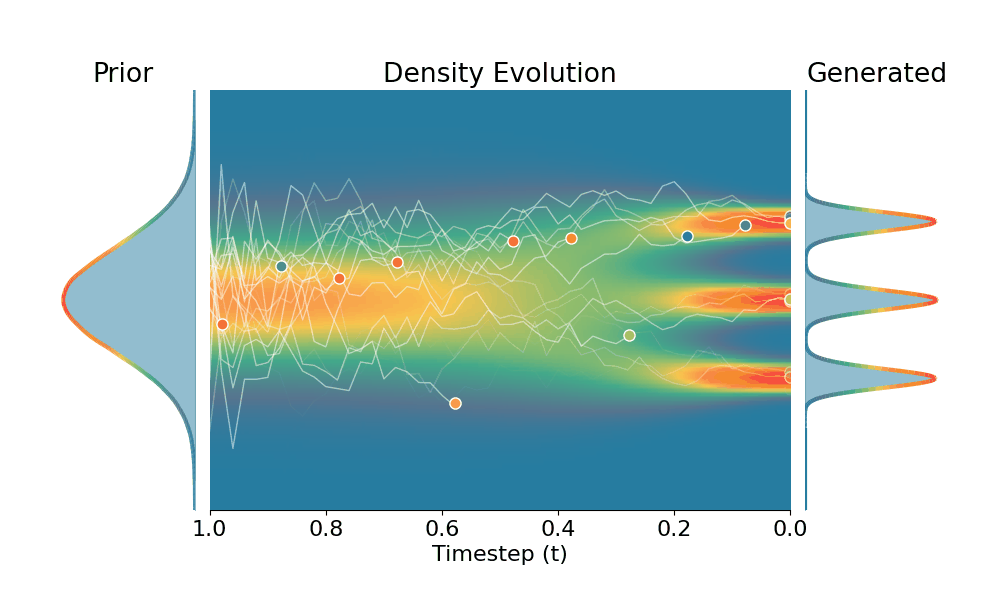
By controling the inverse temperature $k$, we can steer the sampled distribution to be sharper (larger $k$) or broader (smaller $k$). At $k=1$ TSR yields the original distribution.

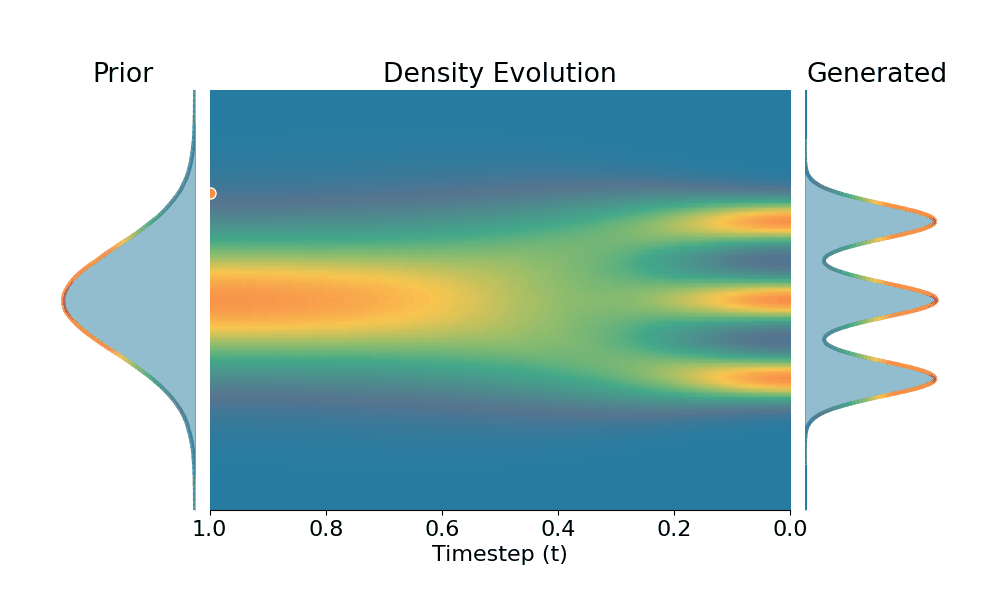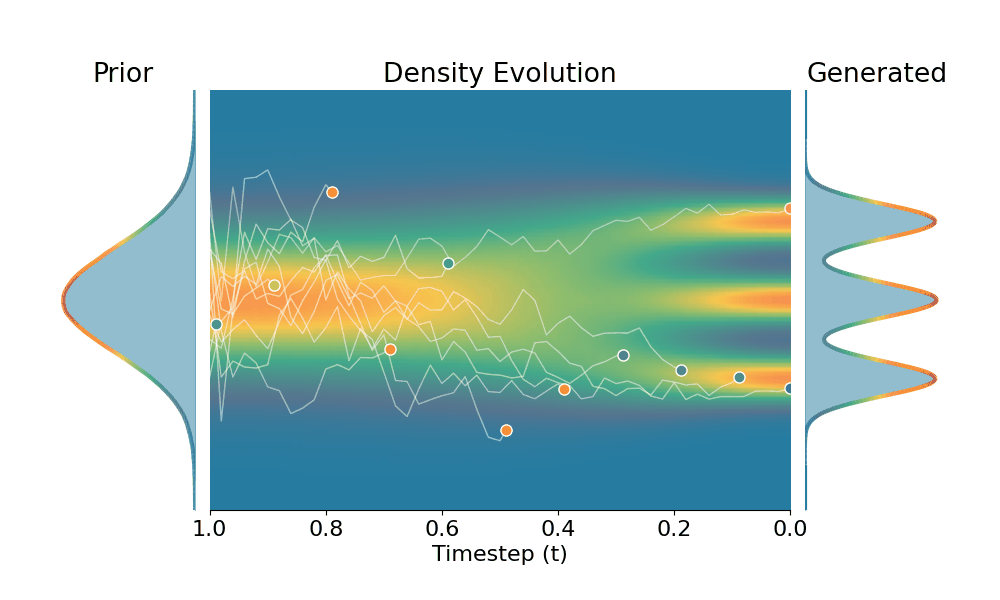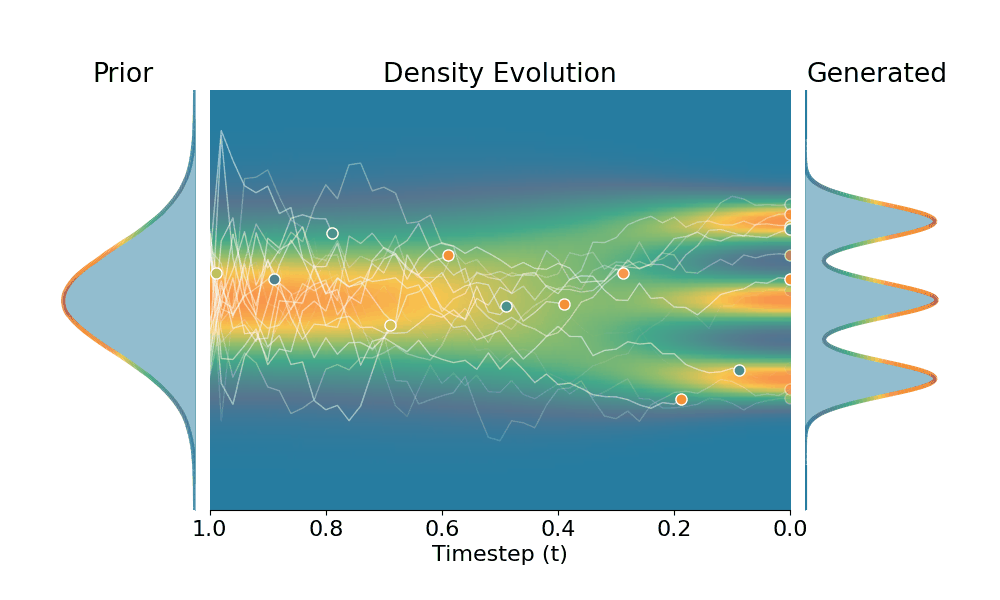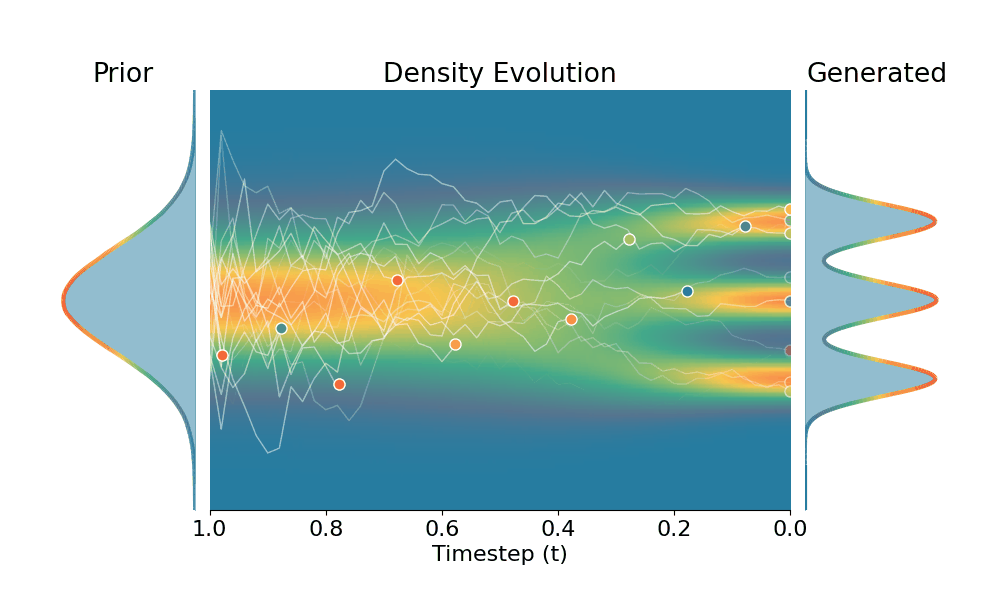
DDPM Unconditional Generation

Original (DDPM)

TSR Unconditional Generation

+Temporal Score Rescaling (Ours)

Drag the slider to control the $k$ values. Each plot shows the prior distribution (left), the probability density evolves over time (middle), and the final generated distribution (right). We also show real sample trajectories during the reverse diffusion process.


Comparison with Prior Methods

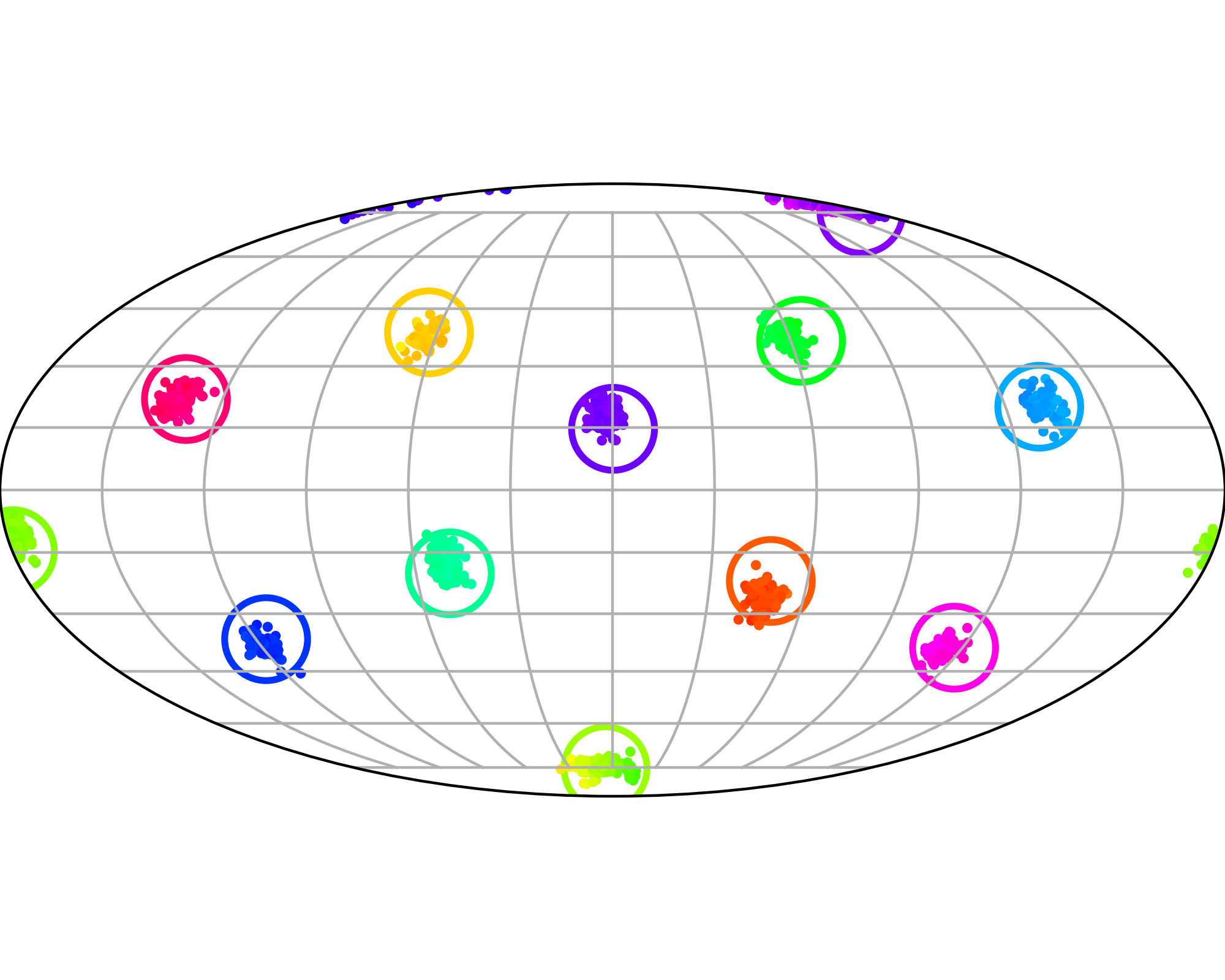
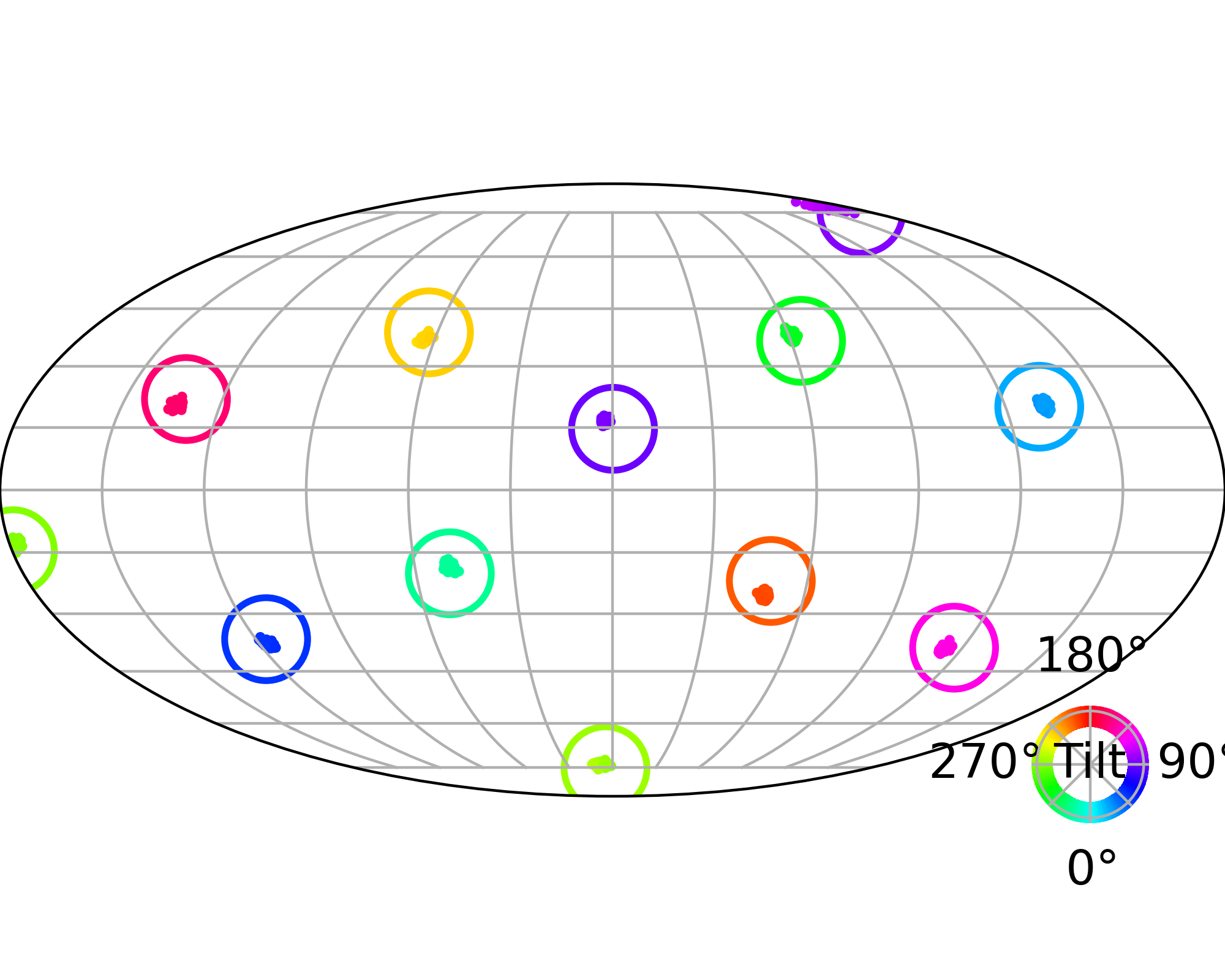
Here we evaluate conditional generation where the data distribution is an isotropic mixture of 6 Gaussians, with the top 3 modes belonging to class 1 and the bottom 3 modes to class 2. We show the sampled conditional distribution for class 1. We compare TSR with Constant Noise Scaling (CNS), the de facto approach for 'pseudo temperature' sampling with diffusion models and Classifier-Free Guidance (CFG). As shown below, both CNS and CFG distort the distribution, while TSR preserves the equal weights between modes. Moreover, CNS does not apply on deterministic samplers (e.g., Flow-ODE), while TSR applies to any diffusion and flow models with any samplers.

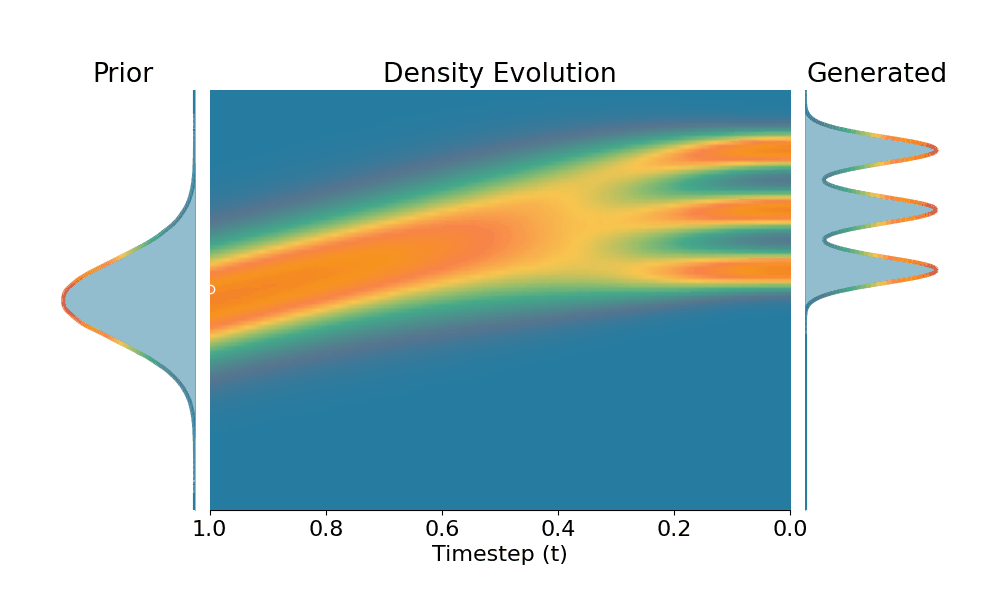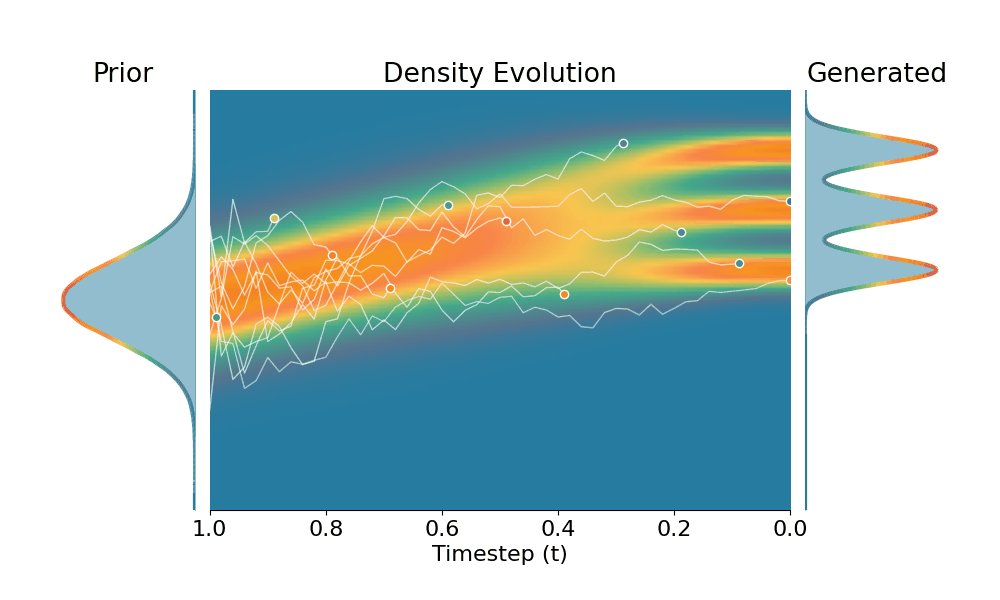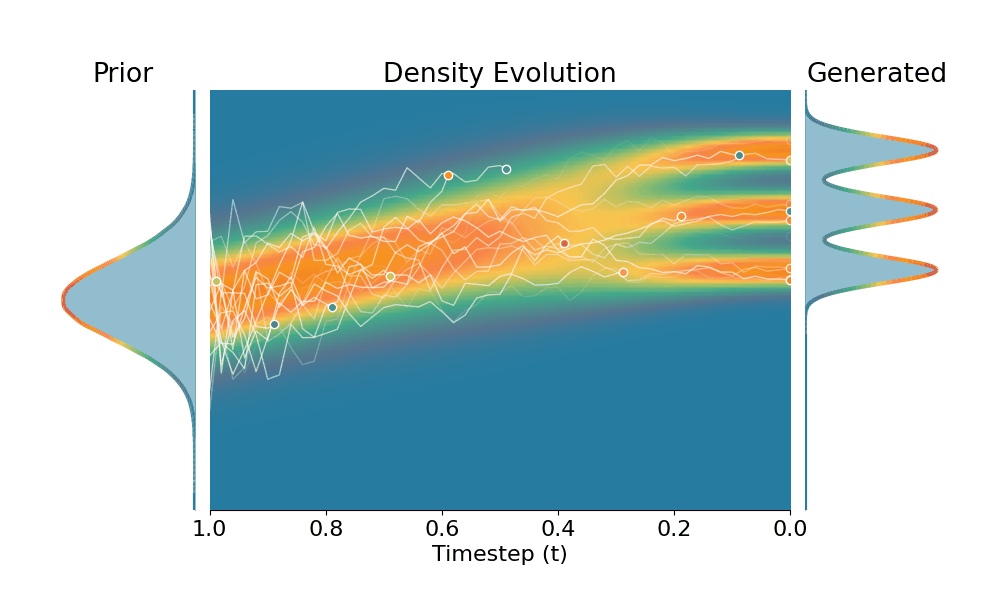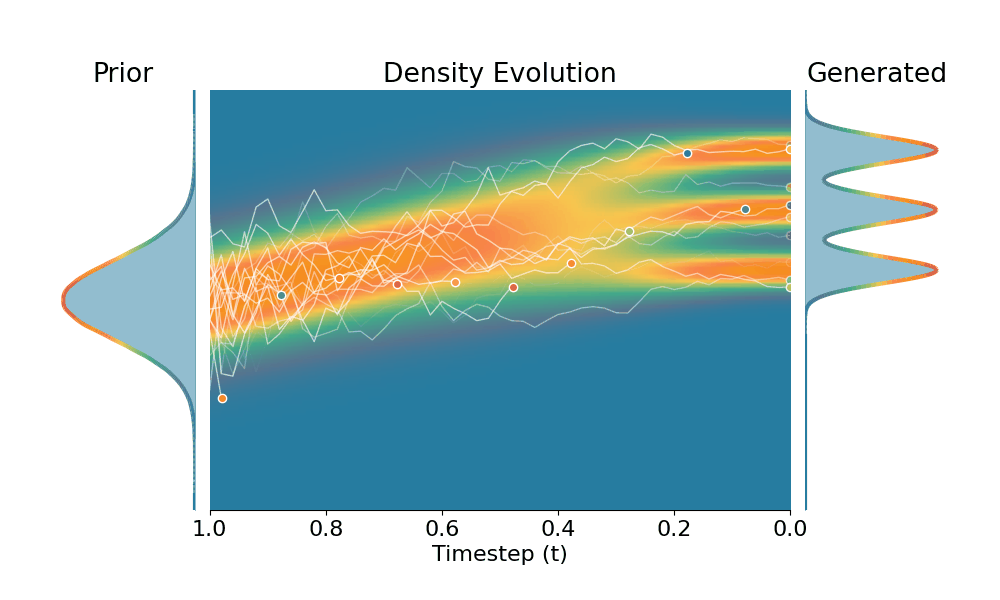
DDPM Conditional Generation

Original (DDPM, class 0)

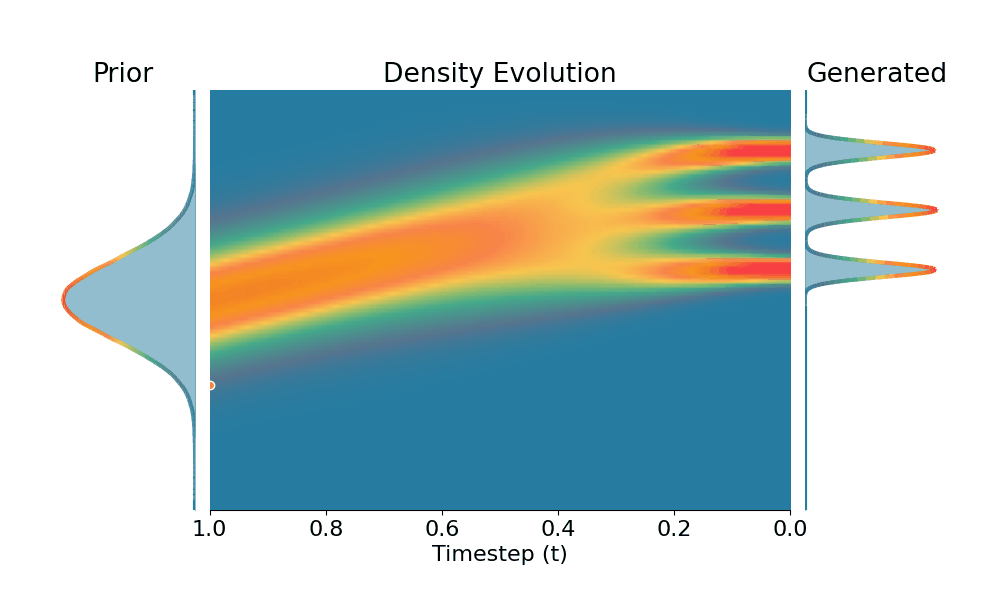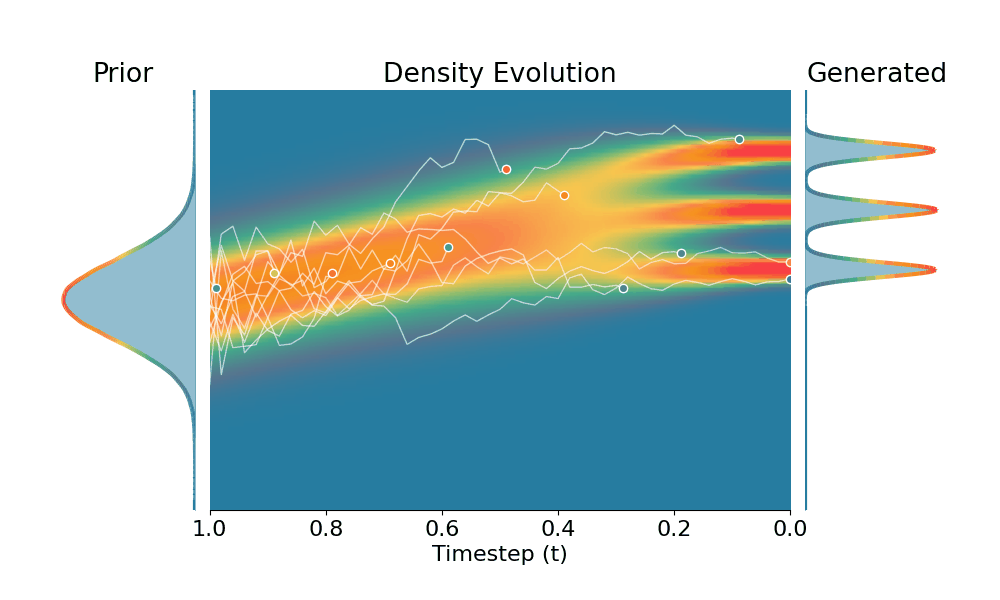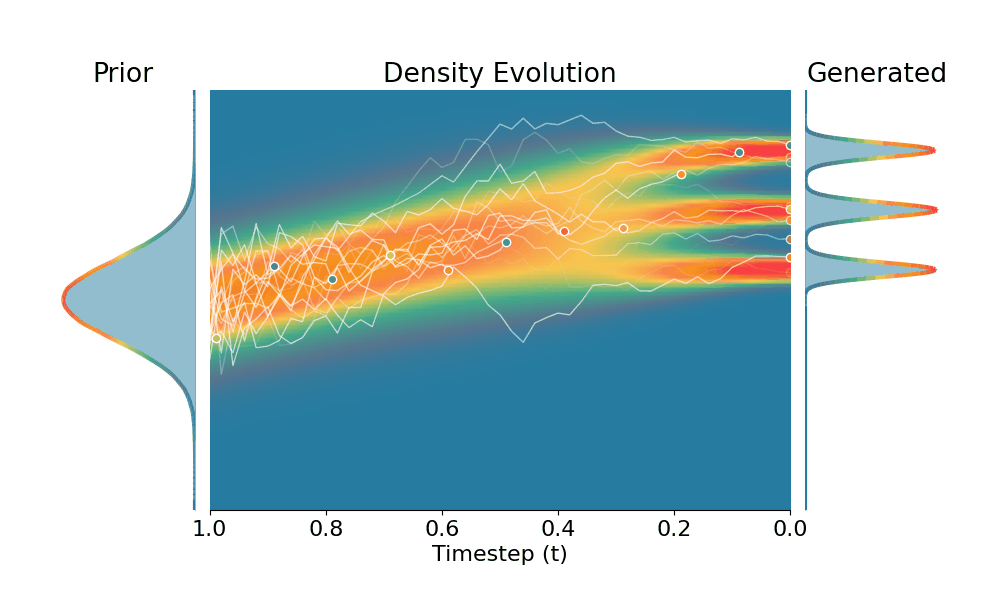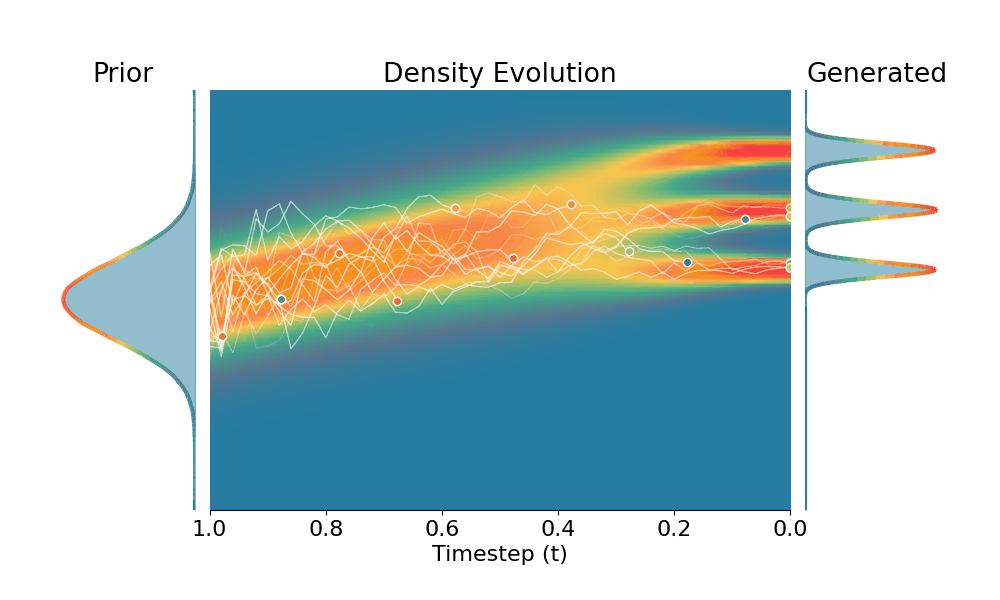
TSR Conditional Generation

+Temporal Score Rescaling (Ours)

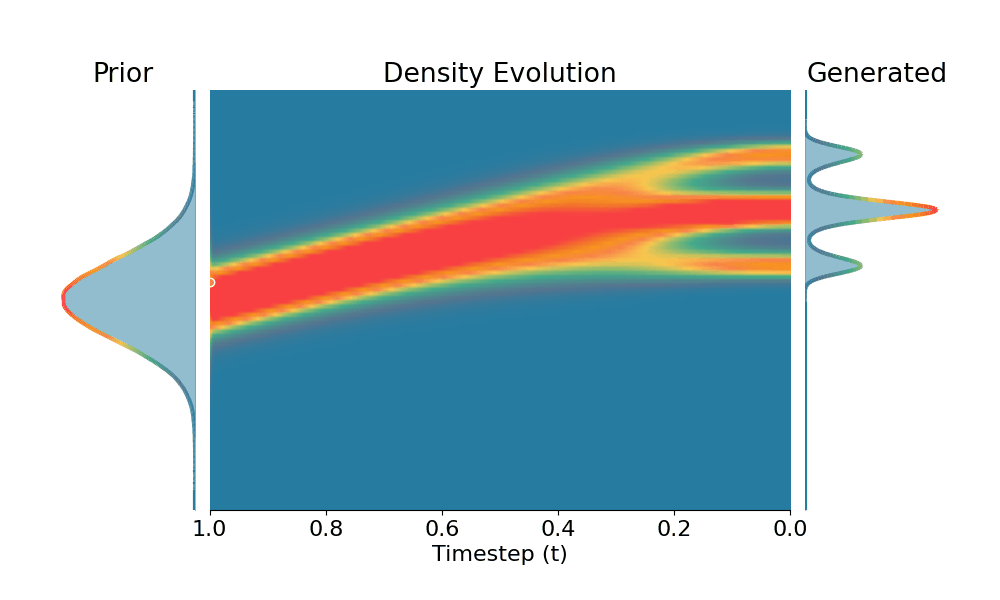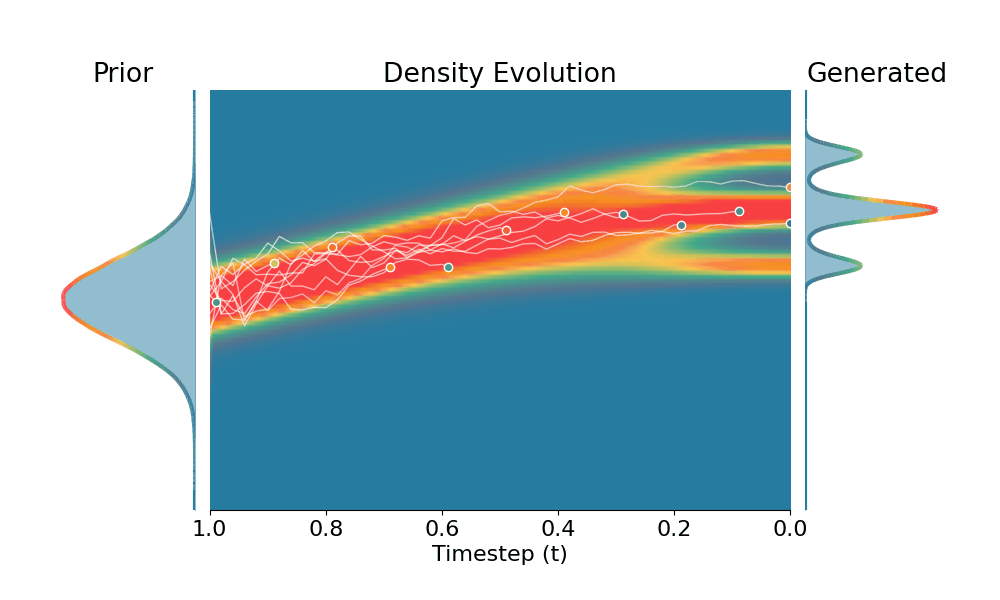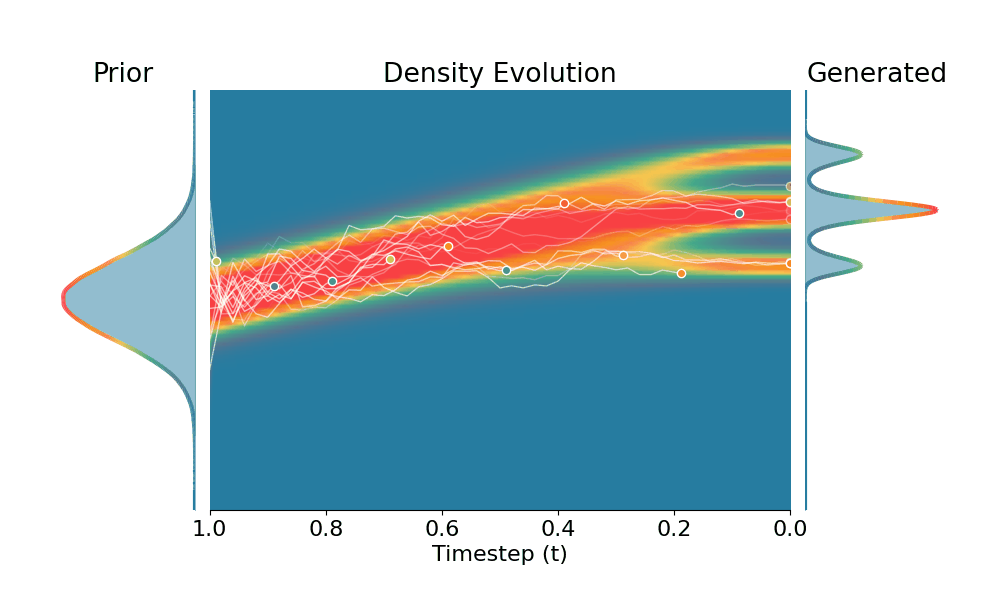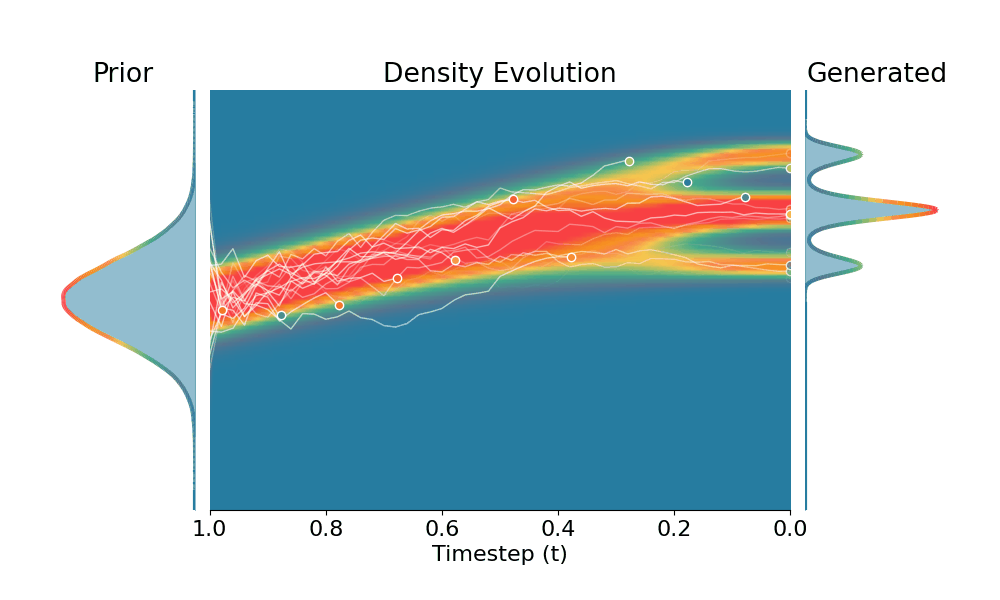
Baseline Conditional Generation

+Constant Noise Scaling

Drag the slider to control $k$ value for TSR and CNS, or the guidance scale for CFG.

The data distribution contains 6 Gaussians with top 3 modes belonging to class 1 and bottom 3 modes to class 2. Showing conditional distribution for class 1.

Comparison on 2D Distributions

Loading visualization data...

Render time: -- | FPS: --

Applications to Real Tasks

We evaluate TSR across diverse applications to demonstrate its versatility and effectiveness. Our method consistently improves sample quality by allowing models to sample from sharper or flatter distributions as needed for each task.

Image Generation

For text to image generation, we find it beneficial to flatten the sample distribution by adopting a $k$ slightly smaller than 1 with TSR. In this way, TSR enhances the high-frequency details in the images and improves both FID and CLIP score.

Original

Original (SD3)

TSR

TSR

TSR applied to Stable Diffusion 3.

Depth Estimation

For depth estimation, we apply TSR to Marigold, a diffusion-based single-view depth estimation model. TSR improves accuracy by sampling from a sharper distribution, yielding less noisy depth predictions.

Input

Input Image

Original

Original (DDIM)

TSR

+ TSR

Depth esstimation results on Marigold.

Object Pose Estimation

Similar to depth estiamtion, TSR improves pose estimation accuracy for geometric objects by reducing uncertainty in orientation predictions.

Input

Input Image

Original

Original (Score Sampling)

TSR

+ TSR

Object pose prediction results on geometric shapes. each dot marks a sample's first canonical axis (colored by rotation), while circles denote ground-truth poses.

Robot Manipulation

We perform comparison on Pi-0 model, which uses flow matching to model the distribution of robot actions. With TSR, the policy achieves better success rate by sampling from a sharper distribution.

Flow Matching

+ TSR